♯Trigonometri dasar

Trigonometri dasar - Halo Bro dan Sis yang cakep-cakep dan baik hati, gimana kabar kalian? Sudah mandikah hari ini? Jangan kayak admin ya, yang mandinya diborong 2 hari sekali. Maklum disini air lagi sulit, xixixi (alibi ngawur). Tentu akan menarik bila kita berbicara tentang Trigonometri dasar karena memang begitu adanya bukan?

Buktinya bro dan sis membaca artikel ini berarti kalian memang sedang mencari informasi terkait Trigonometri dasar. Kami ucapkan welcome alias selamat datang di situs Lemintu. Sebuah situs yang serius dalam memberikan informasi. Daripada admin kebanyakan ngelantur, ada baiknya kita simak saja yuk ulasannya berikut ini.

Pembabaran Lengkap Trigonometri dasar

Artikel ini akan membahas trigonometri dasar, mengenalkan konsep-konsep kunci seperti sinus, kosinus, dan tangen.

Pembahasan akan mencakup penerapan trigonometri dalam mengukur sudut, menghitung panjang sisi segitiga, dan menyelesaikan masalah trigonometri sederhana.

Dengan pemahaman tentang trigonometri dasar, pembaca akan dapat mengaplikasikan konsep ini dalam konteks matematika dan disiplin ilmu lainnya

Mendalam pada Sudut dan Posisi Sudut dalam Trigonometri Dasar

Trigonometri dasar memfokuskan perhatiannya pada hubungan antara sudut dan panjang sisi dalam segitiga, membuka jendela pengetahuan untuk memahami dunia matematika dengan cara yang unik.

Dua konsep kunci yang menjadi fokus utama dalam trigonometri dasar adalah sudut dan posisi sudut.

Sudut:
Sudut adalah pengukuran rotasi antara dua garis atau bidang. Dalam trigonometri, kita umumnya mengukur sudut menggunakan derajat atau radian.

Satu lingkaran penuh setara dengan 360 derajat atau (2\pi) radian. Sudut juga dapat dikelompokkan berdasarkan besarnya, seperti sudut tumpul (lebih besar dari 90 derajat), sudut lancip (kurang dari 90 derajat), dan sudut siku-siku (90 derajat).

Posisi Sudut:
Posisi sudut mengindikasikan lokasi suatu sudut pada lingkaran trigonometri. Lingkaran ini memiliki pusat di titik (0,0) dengan jari-jari satu unit.

Posisi sudut diukur searah jarum jam dari sumbu positif x. Ketika posisi sudut menyentuh satu lingkaran penuh, satu putaran penuh atau 360 derajat tercapai.

Posisi sudut juga dapat diukur dalam radian, dengan satu putaran penuh setara dengan (2\pi) radian.

Fungsi Trigonometri Dasar:
Tiga fungsi trigonometri dasar yang paling umum digunakan adalah sin, cos, dan tan.

Sin θ adalah rasio panjang sisi berlawanan dengan panjang hipotenusa.
Cos θ adalah rasio panjang sisi berdekatan dengan panjang hipotenusa.
Tan θ adalah rasio panjang sisi berlawanan dengan panjang sisi berdekatan.

Melalui pemahaman yang mendalam tentang sudut dan posisi sudut dalam trigonometri dasar

kita dapat membangun fondasi untuk eksplorasi konsep trigonometri yang lebih kompleks dan penerapannya dalam berbagai disiplin ilmu.

Dengan sudut dan posisi sudut sebagai panduan, trigonometri menjadi alat yang kuat dan esensial dalam memahami dunia matematika dan fenomena fisika di sekitar kita.

Membongkar Rumus Dasar Trigonometri: Fondasi Pemahaman Geometri Sudut

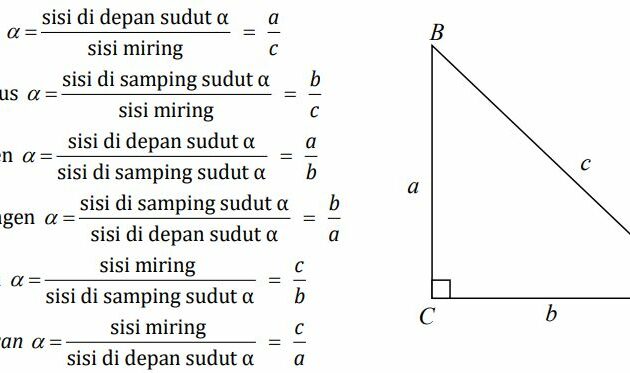
Trigonometri, sebagai cabang matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga, memiliki serangkaian rumus dasar yang membentuk tulang punggung pemahaman trigonometri.

Rumus-rumus ini memberikan rasio panjang sisi dalam segitiga dan memberikan dasar untuk memahami perbandingan sudut dengan panjang sisi.

Identitas Trigonometri Dasar
Sin² θ + Cos² θ = 1: Identitas Pythagoras dalam trigonometri, menunjukkan bahwa kuadrat dari sin θ ditambah kuadrat dari cos θ selalu sama dengan 1.

Rumus Tangen dari Setengah Sudut : Tan (θ/2) = (\sqrt{\frac{1 – \cos θ}{1 + \cos θ}})

Rumus ini berguna untuk menghitung nilai tangen dari setengah sudut berdasarkan nilai cos dari sudut tersebut.

Rumus Sin dan Cos Sudut Jumlah

Sin (α + β) = (\sin α \cos β + \cos α \sin β)
Cos (α + β) = (\cos α \cos β – \sin α \sin β)

Rumus ini memungkinkan kita untuk menghitung nilai sin dan cos dari jumlah dua sudut α dan β.

Identitas Trigonometri Sudut Ganda

Sin (2θ) = (2 \sin θ \cos θ)
Cos (2θ) = ( \cos² θ – \sin² θ) atau (2 \cos² θ – 1) atau (1 – 2 \sin² θ)

Rumus ini memberikan nilai sin dan cos dari sudut ganda 2θ berdasarkan nilai sin dan cos dari sudut θ. Misalkan kita memiliki sudut θ pada lingkaran trigonometri.

Dengan memanfaatkan rumus-rumus ini, kita dapat menghitung berbagai nilai trigonometri yang relevan, termasuk panjang sisi dalam segitiga dan perbandingan antar sudut.

Mengenal rumus dasar trigonometri membuka jalan bagi pemahaman yang lebih dalam tentang konsep-konsep trigonometri yang lebih kompleks.

Penerapan rumus ini secara aktif terjadi dalam berbagai bidang, termasuk fisika, teknik, dan ilmu komputer, membuktikan kepentingan dan keunikan trigonometri dalam memahami dunia sekitar kita.

Membongkar Kebenaran Identitas Trigonometri: Fondasi yang Kekal dalam Dunia Sudut dan Panjang Sisi

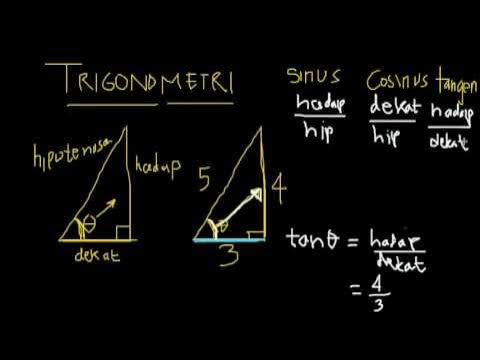
Identitas trigonometri merupakan serangkaian persamaan matematika yang menjadi dasar untuk memahami hubungan antara sudut dan panjang sisi dalam konteks trigonometri.

Dalam eksplorasi ini, kita akan membongkar kebenaran dari beberapa identitas trigonometri yang paling dasar dan berdampak luas.

Pythagoras: (\sin^2 θ + \cos^2 θ = 1). Identitas Pythagoras adalah dasar dari banyak identitas trigonometri lainnya.

Menunjukkan bahwa kuadrat dari sin θ ditambah kuadrat dari cos θ selalu sama dengan 1, identitas ini menarik akar dari sifat-sifat segitiga siku-siku.

untuk Identitas Trigonometri Sudut Ganda

(\sin (2θ) = 2 \sin θ \cos θ)
(\cos (2θ) = \cos^2 θ – \sin^2 θ)
Identitas ini mengungkapkan hubungan antara fungsi trigonometri dari suatu sudut dan sudut ganda tersebut.

Penerapannya luas dalam penyelesaian masalah trigonometri yang melibatkan sudut-sudut yang berbeda.

Identitas Trigonometri Sudut Setengah: (\tan \left(\frac{θ}{2}) = (\sqrt{\frac{1 – \cos θ}{1 + \cos θ}})

Rumus ini memungkinkan kita menghitung nilai tangen dari setengah sudut berdasarkan nilai cos dari sudut tersebut, membuka pintu untuk penerapan dalam berbagai konteks matematika dan ilmu terapan.

Trigonometri Sudut Jumlah:

(\sin (α + β) = \sin α \cos β + \cos α \sin β)
(\cos (α + β) = \cos α \cos β – \sin α \sin β)

Rumus ini menyajikan hubungan antara fungsi trigonometri dari dua sudut dan sering digunakan dalam pemecahan masalah trigonometri yang melibatkan sudut-sudut yang berbeda.

Tangen: (\tan θ = \frac{\sin θ}{\cos θ}). Identitas ini menyatakan tangen sebagai rasio dari sin dan cos, memperluas aplikasi tangen dalam pemecahan masalah trigonometri.

Menggali identitas trigonometri membuka pintu untuk pemahaman yang lebih mendalam tentang hubungan sudut dan panjang sisi dalam trigonometri.

Dengan identitas sebagai panduan, kita dapat menjelajahi dunia trigonometri yang lebih kompleks dan menerapkannya dalam berbagai bidang ilmu.

dalam Identitas trigonometri membentuk fondasi yang kokoh dan esensial dalam matematika dan ilmu terapan.

The post Trigonometri dasar appeared first on RuangBimbel.co.id.

ARTIKEL PILIHAN PEMBACA :

Memuat...

Penutup: Demikian pembahasan lengkap mengenai ♯Trigonometri dasar yang bisa kami sampaikan untuk Anda. Tak lupa kami ucapkan banyak terima kasih karena sudah meluangkan waktu mampir ke situs Lemintu. Kami harap ulasan yang kami sampaikan diatas dapat menjawab rasa penasaran Anda tentang ♯Trigonometri dasar. Bila dirasa pembahasan ini membawa manfaat silahkan share ke teman-teman yang lain. Sampai ketemu di postingan selanjutnya.